A
若 ,答案为 (无需任何操作);
若 ,答案为 (减 即可);
若 为非 偶数,答案为 (直接对 取模);
若 为非 奇数,答案为 (对 取模后减 )。
记得开 long long,时间复杂度 。
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9'){
if(c=='-')f=-1;
c=getchar();
}
while(c<='9'&&c>='0'){
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}
void print(int x){
if(x<0)putchar('-'),x=-x;
if(x>9)print(x/10);
putchar(x%10^48);
}
int t,n;
signed main(){
t=read();
while(t--){
n=read();
if(!n)puts("0");
else if(n==1)puts("1");
else if(n&1)puts("3");
else puts("2");
}
return 0;
}
B
显然有长度为 的超现实子串。
若以 为开头的最长超现实子串长度为 ,根据定义,下一个有潜力成为更优解的 不可能等于 ,其中 。
所以我们只需要扫一遍,对每一个 进行判断,如果能接到之前的就接上去(记录 和 按照定义判断即可),否则回到上一个(特判 的情况)新开一个子串往后继续遍历即可。
最终答案为 ,时间复杂度 。
代码如下:
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9'){
if(c=='-')f=-1;
c=getchar();
}
while(c<='9'&&c>='0'){
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}
void print(int x){
if(x<0)putchar('-'),x=-x;
if(x>9)print(x/10);
putchar(x%10^48);
}
const int N=1e6+5;
int n,a[N],ans,s0,l;
int main(){
n=read();
for(int i=1;i<=n;++i)a[i]=read();
s0=a[1],l=1;
for(int i=2;i<=n;++i){
if(s0+((l+1)&1?-1:1)*((l+1)/2)==a[i])l++;
else ans=max(ans,l),i-=(l!=1),s0=a[i],l=1;
}
print(max(ans,l));
return 0;
}
C
记 dfn[i],siz[i] 分别为第 个遍历到的点和点 的大小。
我们可以确定根,dfn[1] 和最大的 siz[i] 就是根。
考虑 dfs 的过程,遍历每一棵子树类似入栈出栈的过程,考虑用栈来维护整个过程(代码中用数组模拟栈)。
先将根放入栈中,使用消去子树大小的方式判断树的结构。每次用栈顶的子树大小减去下一个 dfs 到的子树大小,并记录下这条边。若删去后子树大小为 ,则该子树已删完。弹出该点,用该点原本子树大小消去栈顶即可。
注意输出时的顺序,时间复杂度 。
代码如下:
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9'){
if(c=='-')f=-1;
c=getchar();
}
while(c<='9'&&c>='0'){
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}
void print(int x){
if(x<0)putchar('-'),x=-x;
if(x>9)print(x/10);
putchar(x%10^48);
}
const int N=1e6+5;
int n,m,dfn[N],siz[N],s[N],tmp[N],cnt;
struct node{
int u,v;
bool operator<(const node &p){
if(u!=p.u)return u<p.u;
return v<p.v;
}
}e[N];
int main(){
n=read();
for(int i=1;i<=n;++i)dfn[i]=read();
for(int i=1;i<=n;++i)siz[i]=tmp[i]=read();
s[++cnt]=dfn[1];
for(int i=2;i<=n;++i){
while(tmp[s[cnt]]==1){
tmp[s[cnt-1]]-=siz[s[cnt]];
cnt--;
}
if(s[cnt]<dfn[i])e[++m]=(node){s[cnt],dfn[i]};
else e[++m]=(node){dfn[i],s[cnt]};
s[++cnt]=dfn[i];
}
sort(e+1,e+m+1);
for(int i=1;i<=m;++i)print(e[i].u),putchar(' '),print(e[i].v),putchar('\n');
return 0;
}
D
观察操作的特点:没有改变元素总和。
考虑很符合直觉的贪心,每次在最大值和最小值上操作直至极差不大于 。
注意: 可以相等,所以操作次数只需要不超过 即可。
证明如下:
考虑一个状态经过一次操作到下一个状态,他们的元素之和相同,我们要保证下一个状态的元素之积比原来的大,否则不需要浪费这一次操作。
在这一次操作过程中,只有两个元素发生变化,其余都可以看成定值,而两个数乘积最大值可由均值不等式取等条件得到,让两个元素趋近相等即可。
上述可以说明每次需要选择一对差值大于 的数进行操作,而可以通过计算比较说明取最值不劣于取任意两值,所以上述贪心成立。
我们只关心全局之积,所以只需要知道最值并且支持插入删除即可,可以用 multiset 维护,不过常数较大(每次需要查询最大值最小值,删除最大值最小值,插入修改后的两个数)。
也可以使用线段树,记录最大值最小值位置,每次只需两次修改,跑得较快。
但是此题应该没有卡常,都可以通过,时间复杂度 。
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9'){
if(c=='-')f=-1;
c=getchar();
}
while(c<='9'&&c>='0'){
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}
void print(int x){
if(x<0)putchar('-'),x=-x;
if(x>9)print(x/10);
putchar(x%10^48);
}
const int N=3e5+5,mod=1e9+7;
int n,m,k,a[N],maxn,minn,ans=1;
struct node{
int maxp,minp;
}t[N<<2];
inline void push_up(int p){
t[p].maxp=(a[t[p<<1].maxp]>a[t[p<<1|1].maxp]?t[p<<1].maxp:t[p<<1|1].maxp);
t[p].minp=(a[t[p<<1].minp]<a[t[p<<1|1].minp]?t[p<<1].minp:t[p<<1|1].minp);
}
inline void build(int l,int r,int p){
if(l==r){t[p].maxp=t[p].minp=l;return;}
int mid=(l+r)>>1;
build(l,mid,p<<1),build(mid+1,r,p<<1|1);
push_up(p);
}
inline void modify(int l,int r,int pos,int p){
if(l==r)return;
int mid=(l+r)>>1;
if(pos<=mid)modify(l,mid,pos,p<<1);
else modify(mid+1,r,pos,p<<1|1);
push_up(p);
}
signed main(){
n=read(),m=read(),k=read();
for(int i=1;i<=n;++i)a[i]=read();
build(1,n,1);
while(k--){
if(a[t[1].maxp]-a[t[1].minp]<=m)break;
a[t[1].maxp]-=m,modify(1,n,t[1].maxp,1);
a[t[1].minp]+=m,modify(1,n,t[1].minp,1);
}
for(int i=1;i<=n;++i)ans=ans*a[i]%mod;
print(ans);
return 0;
}
E
考虑每对 的权值,可以转化成:
怎么求呢,我们使用点分治。
对经过重心的点对路径考虑,处理出 表示点 到重心的距离,一共有 个。
我们只需要记录下来每个 值,按 排序,然后记一下 的子树,按照上式维护 稍微计算即可得到答案。
这是一个 的算法。
可以优化到 ,我们将排序和分治合并。
先递归子树,考虑之后的合并,使用类似哈夫曼树的合并,每次挑两个最小的有序序列合并,可以证明复杂度是正确的,即可得到 的算法。
:
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9'){
if(c=='-')f=-1;
c=getchar();
}
while(c<='9'&&c>='0'){
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}
void print(int x){
if(x<0)putchar('-'),x=-x;
if(x>9)print(x/10);
putchar(x%10^48);
}
const int N=1e6+5,mod=998244353;
int n,head[N],cnt,a[N];
struct node{
int next,to;
}e[N<<1];
void add(int from,int to){
e[++cnt]=(node){head[from],to};
head[from]=cnt;
}
int maxn[N],siz[N],sum,rt,pow2[N],ipow2[N],ans;
bool vis[N];
void get_siz(int x,int fa){
siz[x]=1,maxn[x]=0;
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(y==fa||vis[y])continue;
get_siz(y,x),siz[x]+=siz[y];
maxn[x]=max(maxn[x],siz[y]);
}
maxn[x]=max(maxn[x],sum-siz[x]);
if(maxn[x]<maxn[rt])rt=x;
}
struct NODE{
int val,dis,from;
bool operator<(const NODE &P)const{return val<P.val;}
}b[N];
int Sval1[N],Sval2[N],num,dis[N],Fromnow;
void get_dis(int x,int fa){
b[++num]=(NODE){a[x],dis[x],Fromnow};
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(y==fa||vis[y])continue;
dis[y]=dis[x]+1,get_dis(y,x);
}
}
inline void M(int &x){if(x>mod)x-=mod;if(x<0)x+=mod;}
void dfs(int x){
vis[x]=1,b[num=1]=(NODE){a[x],0,x};
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(vis[y])continue;
Fromnow=y,dis[y]=1,get_dis(y,x);
}
sort(b+1,b+num+1);
int SVal1=0,SVal2=0;
for(int i=1;i<=num;++i){
int Val1=SVal1-Sval1[b[i].from],Val2=SVal2-Sval2[b[i].from];
ans+=1ll*ipow2[b[i].dis]*(1ll*b[i].val*Val1%mod-Val2)%mod,M(ans);
Sval1[b[i].from]+=ipow2[b[i].dis],M(Sval1[b[i].from]);
Sval2[b[i].from]+=1ll*b[i].val*ipow2[b[i].dis]%mod,M(Sval2[b[i].from]);
SVal1+=ipow2[b[i].dis],M(SVal1);
SVal2+=1ll*b[i].val*ipow2[b[i].dis]%mod,M(SVal2);
}
for(int i=1;i<=num;++i)Sval1[b[i].from]=Sval2[b[i].from]=0;
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(vis[y])continue;
maxn[rt=0]=1e9,sum=siz[y];
get_siz(y,x),get_siz(rt,0);
dfs(rt);
}
}
int qpow(int A,int B){
int Ans=1;
while(B){
if(B&1)Ans=1ll*Ans*A%mod;
A=1ll*A*A%mod;
B>>=1;
}
return Ans;
}
void get_pow(){
pow2[0]=ipow2[0]=1;
for(int i=1;i<=n;++i)pow2[i]=(pow2[i-1]<<1)%mod;
ipow2[n]=qpow(pow2[n],mod-2);
for(int i=n-1;i>=1;--i)ipow2[i]=(ipow2[i+1]<<1)%mod;
}
int main(){
n=read();
for(int i=1;i<n;++i){
int u=read(),v=read();
add(u,v),add(v,u);
}
for(int i=1;i<=n;++i)a[i]=read();
get_pow();
maxn[rt=0]=1e9,sum=n;
get_siz(1,0),get_siz(rt,0),dfs(rt);
print(1ll*qpow(2,n)*ans%mod);
return 0;
}
:
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9'){
if(c=='-')f=-1;
c=getchar();
}
while(c<='9'&&c>='0'){
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}
void print(int x){
if(x<0)putchar('-'),x=-x;
if(x>9)print(x/10);
putchar(x%10^48);
}
const int N=5e5+5,mod=998244353;
int n,head[N],cnt,a[N];
struct node{
int next,to;
}e[N<<1];
void add(int from,int to){
e[++cnt]=(node){head[from],to};
head[from]=cnt;
}
int maxn[N],siz[N],sum,rt,ans,pow2[N],ipow2[N],t[N];
bool vis[N];
inline void M(int &x){if(x>mod)x-=mod;if(x<0)x+=mod;}
void get_siz(int x,int fa){
siz[x]=1,maxn[x]=0;
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(y==fa||vis[y])continue;
get_siz(y,x),siz[x]+=siz[y];
maxn[x]=max(maxn[x],siz[y]);
}
maxn[x]=max(maxn[x],sum-siz[x]);
if(maxn[x]<maxn[rt])rt=x;
}
struct NODE{
int val,dis,from;
}b[N];
int Sval1[N],Sval2[N],dis[N],From[N],Fromnow;
void get_dis(int x,int fa){
From[x]=Fromnow;
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(y==fa||vis[y])continue;
dis[y]=dis[x]+1,get_dis(y,x);
}
}
vector<int>p[N],tmp;
void merge(int x,int y){
int px=0,py=0;
while(px<t[x]&&py<t[y]){
if(a[p[x][px]]<a[p[y][py]])tmp.emplace_back(p[x][px]),px++;
else tmp.emplace_back(p[y][py]),py++;
}
while(px<t[x])tmp.emplace_back(p[x][px]),px++;
while(py<t[y])tmp.emplace_back(p[y][py]),py++;
p[x].clear();for(int i:tmp)p[x].emplace_back(i);t[x]=p[x].size();
vector<int>C;swap(tmp,C);
}
struct cmp{
int id;
bool operator<(const cmp &P)const{return t[id]>t[P.id];}
};
void dfs(int x){
priority_queue<cmp>q;
vis[x]=1,p[x].emplace_back(x),From[x]=x;
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(vis[y])continue;
maxn[rt=0]=1e9,sum=siz[y];
get_siz(y,x),get_siz(rt,0),q.push((cmp){rt}),dfs(rt);
}
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(vis[y])continue;
Fromnow=y,dis[y]=1,get_dis(y,x);
}
while(q.size()>1){
int X=q.top().id;q.pop();
int Y=q.top().id;q.pop();
merge(X,Y);q.push((cmp){X});
}
t[x]=(int)p[x].size();
if(!q.empty())merge(x,q.top().id),q.pop();
t[x]=(int)p[x].size();
for(int i=1;i<=t[x];++i)b[i]=(NODE){a[p[x][i-1]],dis[p[x][i-1]],From[p[x][i-1]]};
int SVal1=0,SVal2=0;
for(int i=1;i<=t[x];++i){
int Val1=SVal1-Sval1[b[i].from],Val2=SVal2-Sval2[b[i].from];
ans+=1ll*ipow2[b[i].dis]*(1ll*b[i].val*Val1%mod-Val2)%mod,M(ans);
Sval1[b[i].from]+=ipow2[b[i].dis],M(Sval1[b[i].from]);
Sval2[b[i].from]+=1ll*b[i].val*ipow2[b[i].dis]%mod,M(Sval2[b[i].from]);
SVal1+=ipow2[b[i].dis],M(SVal1);
SVal2+=1ll*b[i].val*ipow2[b[i].dis]%mod,M(SVal2);
}
for(int i=1;i<=t[x];++i)Sval1[b[i].from]=Sval2[b[i].from]=0;
vis[x]=0;
}
int qpow(int A,int B){
int Ans=1;
while(B){
if(B&1)Ans=1ll*Ans*A%mod;
A=1ll*A*A%mod;
B>>=1;
}
return Ans;
}
void get_pow(){
pow2[0]=ipow2[0]=1;
for(int i=1;i<=n;++i)pow2[i]=(pow2[i-1]<<1)%mod;
ipow2[n]=qpow(pow2[n],mod-2);
for(int i=n-1;i>=1;--i)ipow2[i]=(ipow2[i+1]<<1)%mod;
}
int main(){
n=read();
for(int i=1;i<n;++i){
int u=read(),v=read();
add(u,v),add(v,u);
}
for(int i=1;i<=n;++i)a[i]=read();
get_pow();
maxn[rt=0]=1e9,sum=n;
get_siz(1,0),get_siz(rt,0),dfs(rt);
print(1ll*qpow(2,n)*ans%mod);
return 0;
}
F
记 表示以 开头的最长超现实子序列下一个元素的值,这个定义能满足即使不是最长的子序列也可能在之后更新答案。初始时 。
比如初始时 ,而在遇到 后,计算下一个值,,碰到 后 变成 ,以此类推。
我们用集合维护这些 ,具体地说,记 表示 的 所组成的集合。
而遍历到 时,我们将 中的元素代表的 值更新,并从 中删除,插入新的集合中。
上述集合操作可以使用 set,也可以使用复杂度更小的 vector。
最后答案根据每一个 值计算长度取 即可得到。
那么,上述算法的复杂度是多少?我们默认使用 vector。
显然复杂度约等于插入删除的次数,而插入删除的总次数为所有以 开头的最长超现实子序列长度的二倍左右。
考虑在最坏情况下的复杂度,即构造一种最坏情况的序列,假定有 个长度非零的最长子序列,第 个长为 ,首项为 (有 ),不妨设 。
我们定义“附着”表示:两个子序列 ,由于子序列结构的相似性,在 时, 的一多半都可以和 使用相同值(具体长度为 ),那么两者的总长度为 。
将两个子序列表示在二维坐标轴上, 轴表示下标的关系( 相同代表实际下标关系随意, 不同代表下标大小关系), 轴表示值(图中字母无任何含义,由于 ,靠前的是 ,附着的是 ):

然后考虑 个子序列的压缩,显然最坏情况是尽可能多的子序列“附着”在其他子序列上。
对于一个子序列来说,其他每个长度大于它的子序列都能附着约一半的长度。
设有 个不附着在其他子序列上的(长度需要大于附着在它上的子序列长度), 个只附着一半的, 个两边都附着的(会留下一个点)。

例如上图 , 不是的原因是和 值重复。
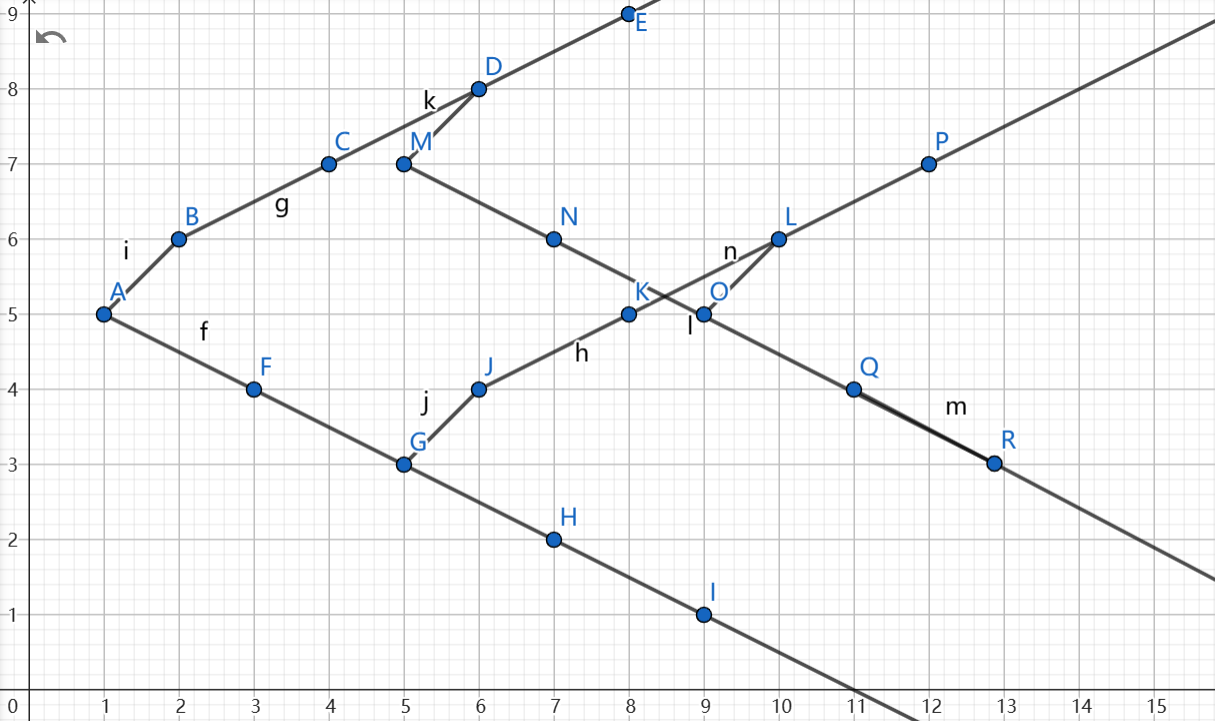
例如上图 , 不是的原因是和 值重复。
由于 ,而 中的最长子序列没有 中的长,不妨把 中的扩大成 中的。
则现在有 中的子序列长度之和加上 中子序列长度之和的一半等于总数 。
所以所有长度之和也是 级别的。
以下是两种能将插入删除次数卡到较大的方法:
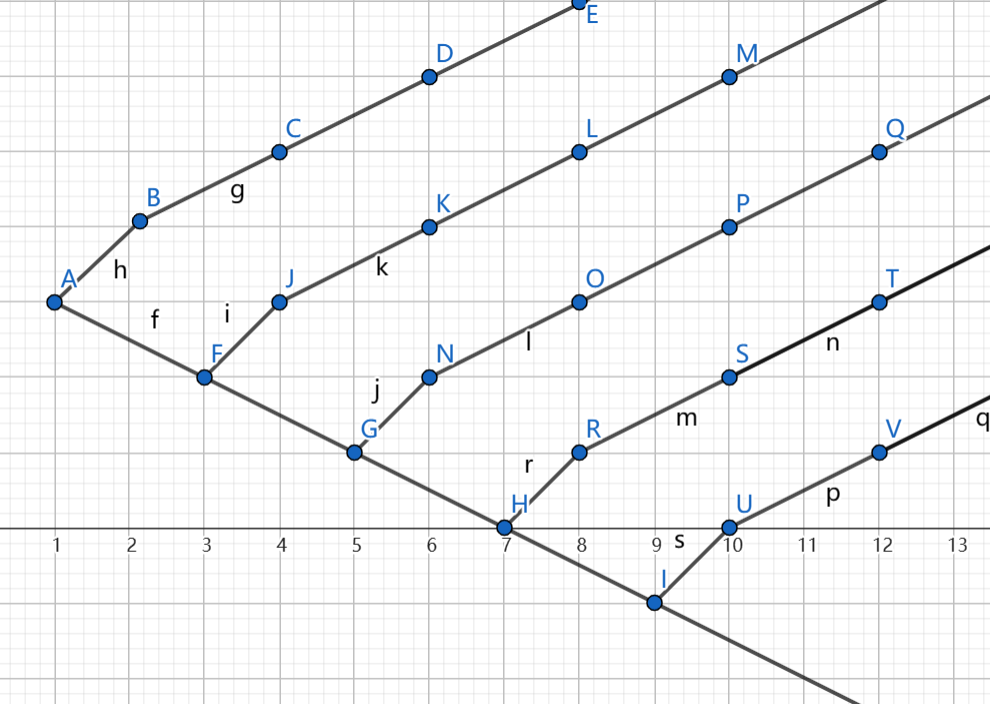
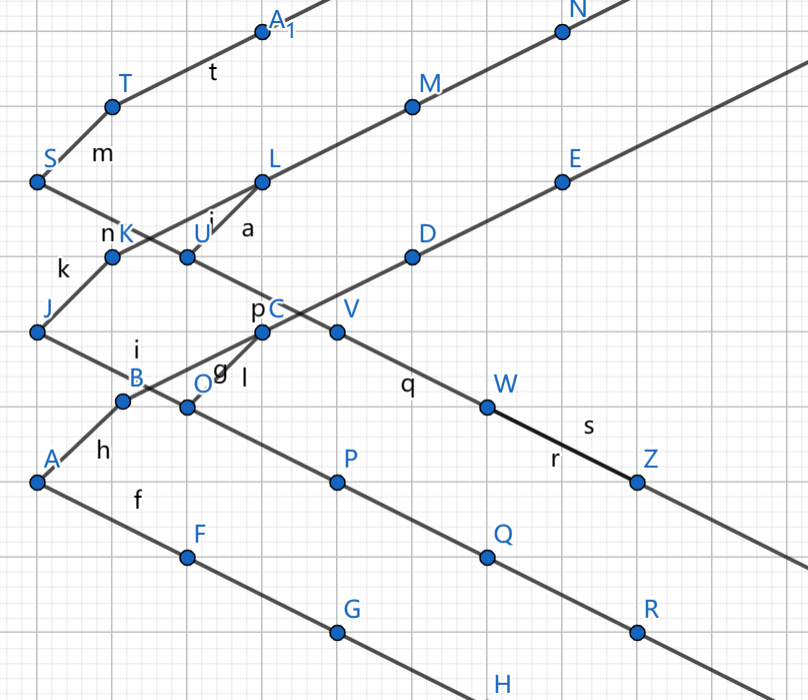
时间复杂度 。
代码如下:
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9'){
if(c=='-')f=-1;
c=getchar();
}
while(c<='9'&&c>='0'){
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}
void print(int x){
if(x<0)putchar('-'),x=-x;
if(x>9)print(x/10);
putchar(x%10^48);
}
const int N=1e6+5;
int n,a[N],nxt[N],k;
vector<int>s[N];
int main(){
n=read();
for(int i=1;i<=n;++i)a[i]=read();
for(int i=1;i<=1e6;++i)nxt[i]=i,s[i].push_back(i);
for(int i=1;i<=n;++i){
while(!s[a[i]].empty()){
k=s[a[i]].back();
nxt[k]=(k<<1)-a[i]+(k>=a[i]);
s[nxt[k]].push_back(k);
s[a[i]].pop_back();
}
}
int maxn=0;
for(int i=1;i<=1e6;++i)maxn=max(maxn,abs(i-nxt[i])*2-(nxt[i]>i));
print(maxn);
return 0;
}










全部评论
(1) 回帖