XOR
时间限制：C/C++/Rust/Pascal 1秒，其他语言2秒
空间限制：C/C++/Rust/Pascal 32 M，其他语言64 M
64bit IO Format: %lld

题目描述

XOR（异或）是一种二元逻辑运算，其运算结果当且仅当两个输入的布尔值不相等时才为真，否则为假。 XOR 运算的真值表如下（表示真，表示假）：

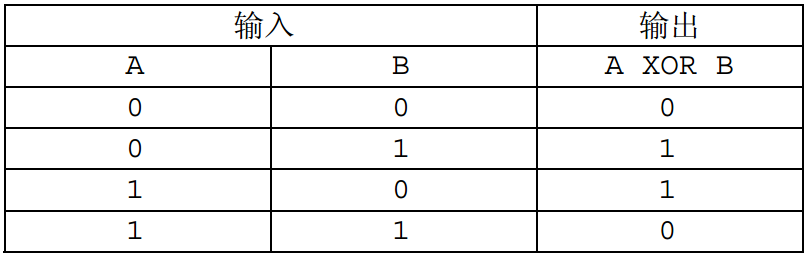
而两个非负整数的是指将它们表示成二进制数，再在对应的二进制位进行运算。

譬如的计算过程如下：

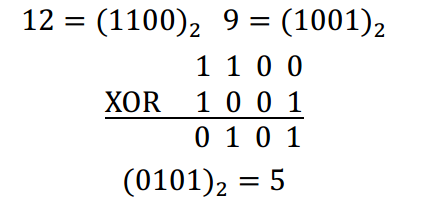
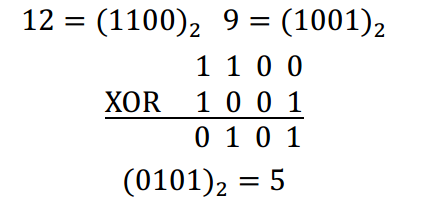
QQ20180128145728.png

故 12 XOR 9 = 5。
容易验证， XOR 运算满足交换律与结合律，故计算若干个数的 XOR 时，不同的计算顺序不会对运算结果造成影响。从而，可以定义 K 个非负整数 A_KA的 XOR 和为

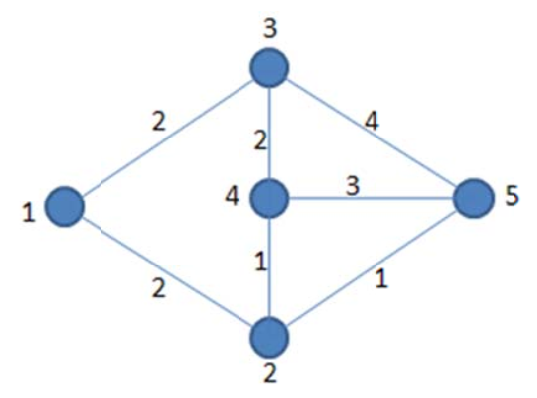
考虑一个边权为非负整数的无向连通图，节点编号为 1 到 N，试求出一条从 1 号节点到 N 号节点的路径，使得路径上经过的边的权值的 XOR 和最大。
路径可以重复经过某些点或边，当一条边在路径中出现了多次时，其权值在计算 XOR 和时也要被计算相应多的次数，具体见样例。


输入描述:

第一行包含两个整数 N 和 M， 表示该无向图中点的数目与边的数目。
接下来 MM 行描述 MM 条边，每行三个整数 S_i,T_i,D_i,表示 S_i 与 T_i之间存在一条权值为 D_i的无向边。
图中可能有重边或自环。

输出描述:

仅包含一个整数，表示最大的XOR和（十进制结果）
示例1

输入

复制 
5 7 
1 2 2 
1 3 2 
2 4 1 
2 5 1 
4 5 3 
5 3 4 
4 3 2

输出

复制 
6

说明

QQ20180128150132.png
如图，路径1 \rightarrow 2 \rightarrow 4 \rightarrow 3 \rightarrow 5 \rightarrow 2 \rightarrow 4 \rightarrow 5对应的XOR和为
2 \ XOR \ 1 \ XOR \ 2\ XOR\ 4 \ XOR\ 1 \ XOR\ 1 \ XOR \ 3 = 6
当然，一条边数更少的路径1 \rightarrow 3 \rightarrow 5对应的XOR和也是2 XOR 4 = 6。

备注:


对于  的数据，， ，；
对于  的数据，，，；
对于  的数据，， ，；
对于  的数据，， ，。